這邊引用上課教材來說明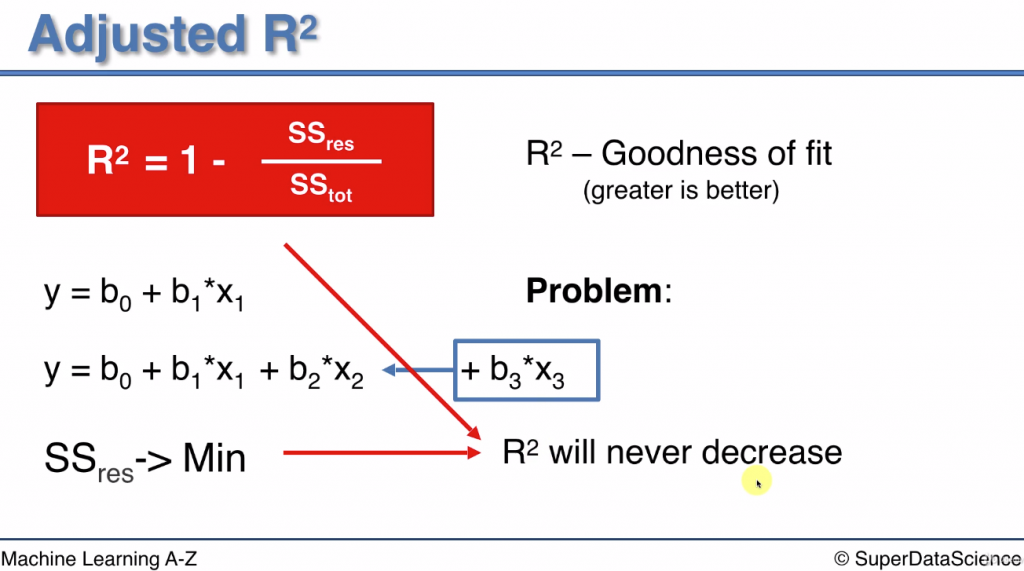

問題：
原本的Ｒ平方： 目標是找b0, b1, b2 參數使得剩餘平方和最小
現在：增加一個自變量到多元線性模型中, 擬合效果會變好還是變差？ Ｒ平方會變大還是變小
結論： 新增自變量, 擬合效果不會變差, Ｒ平方永遠不會降低（和之前相同or更高）
為什麼：
假如可以找到一個b3 使得剩餘平方和變小, SSres/SStot 也會變小(分母不變), 那R平方就會變大
假如找不到一個b3可以使得剩餘平方和變小, 但最差情況下b3可選擇0
此時頂多相當於這個自變量沒有加, 所以Ｒ平方不會降低

Example:
假設x3=員工當月月績, 那新增x3 對薪資的擬合度就越高, R平方會增高, 因為可以通常月績和薪資也有一定的關係
假設x3=員工手機末三碼, 顯然跟員工薪資沒有關係, 但擬合出來的b3其實不會等於０, 會趨近於0(因為是用數學來擬合, 或多或少手機號碼和薪資有一些數學上的關係), 但這顯然和常理不符
R平方就算有上升也不代表對模型有更好的精準度
所以廣義的Ｒ平方也將變數的數量納入考慮

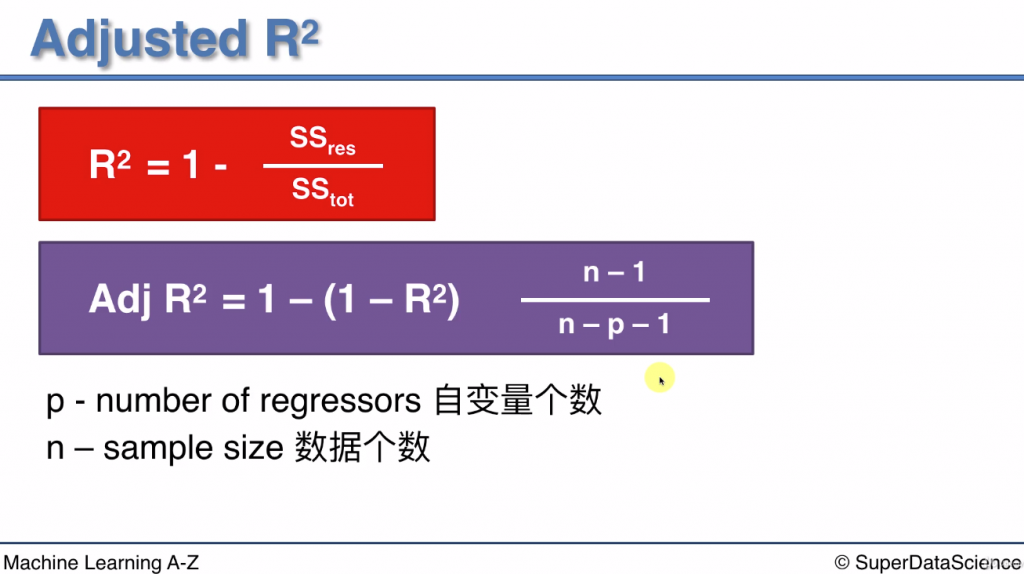
p: 自變量個數
n: 數據集中有多少點(數據個數) (和模型無關)

讓我們搭配顏色來推倒當新增變數會發生什麼事？
(紅色)當新增一個變數, p會變大
(灰色)n-p-1 會減少, n-1/n-p-1 就會變大
(藍色)因為新增變數所以依照原本Ｒ平方特性,Ｒ平方變大
(紫色)1-R平方變小
最關鍵的(紫色)下降(灰色)上升, 所以整個廣義Ｒ平方結果不一定會升高或降低

當新增手機末三碼這個變數後, (紫色)下降的幅度沒有(灰色)上升幅度多的時候, 可能導致廣義Ｒ平方下降, 此時就能反映出這個變數會降低精准度的事實